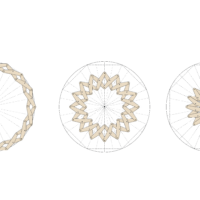
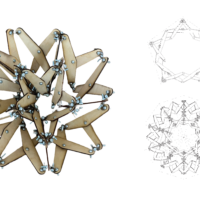
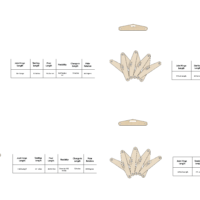
Mathematical influence begins to translate within the forms of everyday objects to interpret the physical world and structures, making the construction of architectural design possible. This is achieved by dissecting how geometries are extracted from polyhedrons in two-dimensional space and how they transition from lines and points into kinetic three-dimensional objects. Chuck Hoberman offers adaptability by utilizing the polyhedron’s geometric characteristics. How can Hoberman’s spherical system be analyzed and re-engineered in order to invite more diverse usages that provide technological advancements for adaptive systems? 

This research question aims to dissect the construction of the Hoberman sphere and utilize its structural characteristics to repurpose the scissor joint mechanism into a unique system. Through architectural intervention, the change within the original system serves as a guideline by establishing new properties, conditions, and characteristics to work from. Computational algorithms serve as a method to visualize movement leading to the construction of digital representations.

A series of tests using fabrication techniques explore changes within the system through prototyping, documenting, and analyzing its conditions. This framework of investigation explores the possibilities of the scissor mechanism proposed by Hoberman, while challenging how alterations can influence its assembly when scaling up to architectural construction.