The Urban Genome Project

Month: February 2021

Venues can unsettle sedimented patterns of segregation under certain conditions: addendum to “Venues and segregation: A revised Schelling model”

February 5, 2021 / / 0 Comments

line
Generative models of urban form

In Venues and segregation: A revised Schelling model we demonstrate that venues can play a crucial role in shaping urban evolution, in particular through influencing broader patterns of integration and segregation. Due to space considerations, we could not include a key study in the paper.

This study investigates whether and how venues can diversify a segregated city after it a particular segregation pattern has become deeply entrenched. To answer this question, we first simulate a highly segregated city as an outcome of a standard Schelling process. Then we use a genetic algorithm to evolve the set of rules that would most decrease the degree of segregation. These rules include the location of venues, their exclusivity, and their degree of obligatoriness. In effect, the study evolves rules that would most dramatically alter the evolutionary direction of a city.

The study is below. See the original paper for more details regarding the parameters and graphical conventions, and simulation rules. 

Venues can unsettle sedimented patterns of segregation under certain conditions.

In this study, we demonstrate that the strategic placement of a new venue can unsettle sedimented patterns of segregation. This is important because one of the characteristics of the segregation patterns generated in Schelling simulations is that they are highly uni-directional processes. Once a set of individuals has become segregated, even a significant increase in their tolerance will not undo the neighbourhood divisions that have taken shape – barring any modifications to the internal psychology of individuals within the simulation. In this study, we show that venues can be used as an intervention within a settled Schelling model in order to disrupt the segregated outcome, without requiring any change to agents’ psychology. To do so, we add venues to a venue-less simulation that has already run its course and achieved a high level of segregated stability. In order to effectively determine what input parameters and venue positions will provide the most disruption, the two-dimensional parameter spaces used to explore earlier studies is not sufficient. Here we consider a range of venue positions, exclusivity, obligatoriness, tolerance, travel distance, and neighbourhood distance values simultaneously. In lieu of our prior interval based approach, we employ a Genetic Algorithm to test and recombine values for these parameters, evaluating different combinations in terms of how much they disrupt the initial condition (measured as a drop in concordance from the initial, segregated condition). An additional mechanism emerges, whereby one group’s venue establishes a “beachhead” into an area predominated by the other.

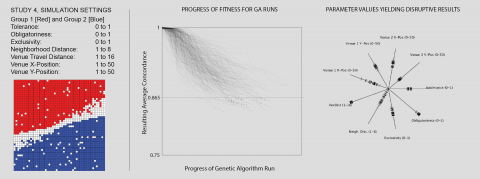
Figure 1 displays results. After running the algorithm with a variety of population sizes, mutation rates, and crossover rates, the progress of each evolutionary process is mapped as a sequence of fitness values to the chart in center of Fig 1.  Here, movement towards the right along each thread indicates the progress of the algorithm during one of its runs, while dropping values on the Y-axis indicate a reduction in the resulting concordance, i.e. a more successful solution. We select the most successful interventions in order to compare their values for each input parameter in the chart to the right in Fig 1.  Here, each notch along one of the spokes indicates a parameter value for one of the interventions, and hence, each intervention can be composed from a set of notches on each of the spokes.

FIG 1 HERE.

Beginning from “Intolerance” and working clockwise through the spokes on Fig. 1, we consider the significance of the values arrived at for each, highlighting values that contribute to disruptive solutions. Overall, these solutions cluster around medium-low intolerance levels, high obligatoriness, middling exclusiveness, high catchment areas, a wide range of neighbourhood distances, and “beachhead” venue positions.

Intolerance: The intolerance values are clustered tightly around the value of 0.4 in successfully disruptive solutions. This value, just above the traditional Shelling tipping point, can be understood as a trade-off: it is high enough to motivate some movement by individuals, but low enough to support these same agents moving to an integrated rather than segregated destination.

Obligatoriness: The obligatoriness values tend towards 1 in disruptive solutions. Since obligatoriness controls the fraction of individuals that will feel compelled to visit venues, and since venues are the mechanism for disrupting the settled state, it follows that maximizing venue attendance will maximize the potential disruption. By contrast, introducing venues that inspire no obligation to attend them will do little to alter a segregated condition.

Exclusivity: Since exclusivity controls the number of other-group individuals who will consider visiting a venue, it regulates the new encounters between the segregated groups. It follows that an exclusivity of less than 1 is necessary in order to yield any new outcomes.  On the other hand, if the exclusivity is too low, any agents within the travel distance would visit and it would hence replicate the distribution of the surrounding area. Between these extremes, and in fact closer to an exclusivity range from 0.4 to 0.6, we have circumstances in which some individuals of the opposite group will be drawn into a venue, leading to a disruption when they find that after visiting they are no longer comfortable with their location. Thus maximizing disruption involves introducing venues that are neither too exclusive nor too open but rather those that exist in a “sweet spot” between the two extremes.

Neighbourhood Distance: The neighbourhood distance is the most dispersed of the non-location parameters, with all of its distribution occurring below a value of 4. We interpret this to imply that neighbourhood distance does not play a significant role in the outcome, so long as it is sufficiently low.

Venue Travel Distance: Unlike neighbourhood distance, the venue travel distance is very tightly clustered, and tends towards the highest value possible.  Since venue travel distance directly determines the number of individuals who can be affected by the venues, higher values naturally yield more disruptive results. Thus introducing venues with large catchment areas is likely crucial to interventions designed to unsettle existing patterns of segregation.

Venue Positions: Each of the two venues’ positions are encoded as an X and Y value between 1 and 50. This allows them to be located anywhere in the simulation world, even if this means displacing an individual from their initial condition. While their positions in successful solutions are mostly constrained to a narrow range, the X position of the first venue is something of an exception – with a whole range of positions that yield disruptions. In Fig 2, we summarize our findings for the venues’ positions by stepping through each cell, finding any simulations in which one of the venues occupies this cell, and colouring the cell according to the most disruptive outcome from among these simulations. In other words, we colour each square according to a best-case scenario of having a venue located there.  What results is a map of the most effective positions for locating venues.

FIGURE 2 HERE.

Venues at “beachheads” are most likely to disrupt stable segregation patterns.Though the central map of Fig 2 clearly illustrates that there is a broad band of more successful venue locations along the boundary area between the two segregated groups, closer inspection reveals that ideal positions tend to be slightly embedded within one of the groups, rather than in the unoccupied space between. The tight clustering of values for the other parameters suggest that the successful disruptive runs are all variations on a single, emergent, strategy.  This strategy involves locating a relatively open venue of a group (G1) near to the edge but slightly embedded within the segregated neighbourhood of the opposite group (G2).  Because of the high maximum travel distance, individuals from the G1 are able to visit from farther away, while some closer agents from G2 are welcomed by the low exclusivity.  Upon visiting, these G2 agents become less comfortable with their location, since attendance has exposed them to a greater number of agents from G1. Simultaneously, the opposite dynamic is unfolding somewhere else in the simulation world. Because of this symmetry, individuals from both groups who feel compelled to move will find new locations opening up within travel distance to an appropriate venue, leading to an exchange between two areas of the simulation world.  Since the venue exclusivity is not too low, this exchange is not a complete flip – only the fraction of individuals who visit the opposite venue will relocate. These venues act like a “beachhead”, pushing away individuals from the other group and opening up spaces for their own agents to occupy. We can watch this same dynamic unfolding in the Video.

Summary

In this study,  we consider the possibility of applying our venue model as an intervention in highly segregated conditions. The success of the genetic algorithm in finding highly disruptive venue configurations speaks to the potential role for planning and design as a means of re-integrating a divided urban condition.  It must be stressed that the successful strategy described in this study is specifically tuned to the particular starting conditions that were used. Nonetheless, this study points at specific spatial relationships between segregated groups and disruptive venues as well as the crucial balancing of parameters such as intolerance and exclusivity. Further research would be necessary to generalize these results for other kinds of initial distributions of the simulated population.

New paper published! Venues and segregation: A revised Schelling model

February 5, 2021 / / 0 Comments

line
Generative models of urban form

simulations

It goes without saying that most of our lives are spent in buildings. Less obvious are the implications of this obvious fact.

Consider a two-dimensional map. It presents a smooth surface, but the reality it represents is warped. Certain points on it support more interaction than others: the ones with buildings on them. Being near such a point puts you in close contact with more people than elsewhere. Depending on the social rules governing who is supposed to be there and what they are supposed to do, the building may increase or decrease your chances of coming into contact with people similar to or different from yourself.

They are not just physical structures, they are venues for social life, and the social order of cities grow up around them. If they change — their number and distribution, their rules of social inclusion or exclusion, the types of activity they afford — the city changes as well. This combination of forms, groups, and activities is the anchor of our model of urban evolution. 

In a new paper (with Ultan Byrne and Patrick Adler), we show via computer simulations the power of venues to affect the broader urban order by shaping the interactions of individuals. We do so by building upon the classic work of Thomas Schelling/ In 1971, Schelling proposed what became known as the “Schelling model of segregation,” which expressed in an especially clear way the type of thinking for which he eventually received the Nobel prize: local, small-scale interactions generate larger aggregate structures, often in surprising ways.

The “Schelling model of segregation” shows this vividly. Imagine a checkerboard with red and blue pieces that represent individuals. Let’s say each individual has a desire to be around people of their own group. Let’s make it relatively small: a red individual wants at least 25-30% of the others around them to be red, otherwise the’ll move to a different location where this condition is met, if they can.

Schelling showed that, starting from a random distribution of reds and blues, if you repeat this process over and over again you’ll end up with basically total segregation of red and blue. The map that results looks eerily like real cities.

The irony is that, within the Schelling model, no individual agent wants this outcome. The social structure is not necessarily a direct result of individual intentions. Moreover, once that pattern of segregation sets in, outside of a radical transformation of human psychology, little can be done to alter it (within this model).

This is a model and like any model it makes many simplifying assumptions. In our paper, we think through the implications of something maybe so simple that prior studies of this model have largely overlooked: there are no buildings in it, it does not capture the warped space we live in.

So we built a model that extends Schelling’s to include buildings in the simplest way we could think of. Basically, you need four things: 1. a travel radius (how far your reds and blues will go to visit the venue); 2. exclusivity (is the venue exclusive to one group, like an exclusive golf club, or is it open to members of any group); 3. obligatoriness (are individuals obliged to attend it, like an orthodox synagogue, or is it more optional, like a cafe); 4. physical features (how many venues are there, and where are they located).

With those simple features, you can account for, and observe the logical implications for urban segregation and integration, of one of the most pervasive facts of our experience, which is that we congregate in buildings. This happens because the people you interact with in buildings alter the Schelling-style calculation as to whether an individual feels “comfortable” in their location. One might be a majority in terms of the people who live nearby or who you pass by on the street, but a minority when you include those you meet in the venues. Or vice versa: you might be a minority in terms of who lives there, but interact with many people of your group in the local venues (who traveled there from elsewhere) or travel elsewhere to interact with members of your group.

By repeating and varying those simple processes you can think through their implications. One is that they generate a distinctively urban order: Schelling’s model yields clumps whose physical location has no meaning or basis. With buildings in the model, you can generate an East vs. West side (“opposite sides of the tracks”) or a centre-periphery structure with a more diverse core and more homogenous peripheries.

You can also observe how, depending on the characteristics and location of the building, it is possible to forestall the deep segregation characteristic of the Schelling model from arising, without requiring any radical transformation of individuals’ psychology. You can also unsettle deeply sedimented patterns of segregation through the right combination of venue parameters, whereas they are basically set in stone in Schelling’s highly individualistic model (via a genetic algorithm, not shown in this paper but coming to a blog post soon)

And you can find ironies and reversals like the sort Schelling exposed. Just as Schelling demonstrated that one cannot simply read individual intentions from collective patterns of behavior, one cannot simply read organizational values from their surrounding patterns of segregation. Relatively exclusive venues can generate diverse neighborhoods (by providing a local foothold for minority groups to sustain their distinctive cultures), while relatively inclusive venues can in some circumstances produce highly segregated areas (by drawing in tolerant and “adventurous” persons who, despite their individual understanding, change the overall makeup of the area).

An advantage of the computer simulation approach is that you can pinpoint the precise mechanisms by which these outcomes occur. Some of these include “evacuation,” “cooptation,” “bootstrapping,” “cascading,” and “bridging.” 

The paper also includes videos showing the simulation runs unfold. 

The abstract is below. The paper is freely available here.

Abstract: This paper examines an important but underappreciated mechanism affecting urban segregation and integration: urban venues. The venue- an area where urbanites interact- is an essential aspect of city life that tends to influence residential location. We study the venue/segregation relationship by overlaying venues onto Schelling’s classic (1971) agent-based segregation model. We show that a simulation world with venues makes segregation less likely among relatively tolerant agents and more likely among the intolerant. We also show that multiple venues can create spatial structures beyond their catchment areas and that the initial location of venues shapes later residential patterns. Finally, we demonstrate that the social rules governing venue participation alter their impacts on segregation. In the course of our study, we compile techniques for advancing Schelling-style studies of urban environments and catalogue a set of mechanisms that operate in this environment.

Daniels Logo Daniels Logo

© 2024 THE URBAN GENOME PROJECT, UNIVERSITY OF TORONTO

— Up ↑