One key way that evolutionary processes occur is via feedback loops. A classic way to model such feedback loops is in functional terms. Arthur Stinchcombe articulated the elemental structure of functional explanations in his 1968 book, Constructing Social Theories. In our recently published article, “Complex causal structures of neighbourhood change,” we try to revive this model and demonstrate its value for studying the evolution of cities.
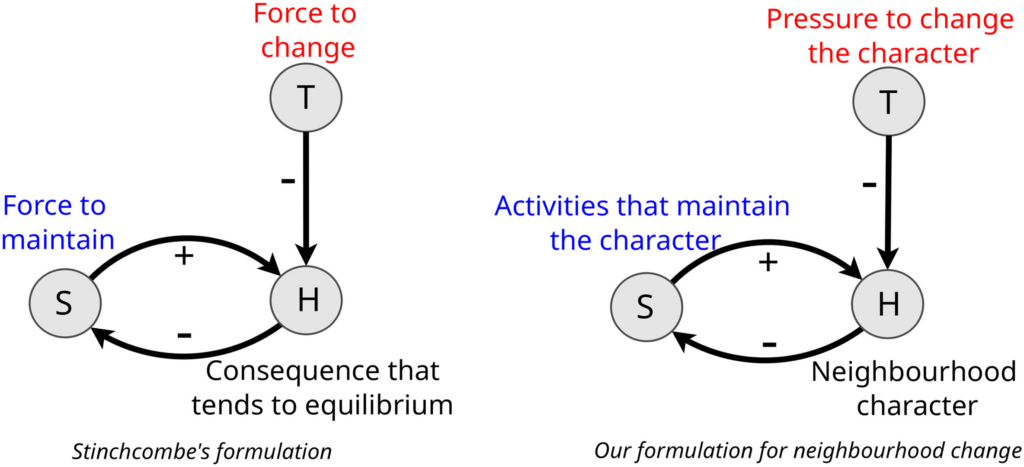
The above figures shows Stinchcombe’s model on the left, and our reformulation of the model for neighbourhood evolution. It codified the causal structure of a complete functional explanation in terms of four core elements:
- The consequence that tends to be maintained, which also functions indirectly as a cause of the behaviour or social arrangement to be explained. This is H, the “Homeostatic” variable. Though H may tend to be stable empirically, its stability is maintained against pressures to change it, such as in the case of body temperature.
- The social arrangement or behaviour that impacts H, the explanandum. This is S, the “Structure.” In a functional model, Structures tend to maintain Homeostasis. For example, sweat glands tend to maintain body temperature.
- Tensions that tend to upset Homeostasis, unless Structures maintain it. This is T, the “tension” variable. If physical activity or air temperature did not alter body temperature, there would likely be no structure to counteract the tensions they create.
- Processes that reinforce or select for the S’s (structures) that maintain H (homeostasis). When H is threatened or pressured, these forces increase the activity of S when T (tensions) are higher and decrease when H is maintained. For example, sweat glands generate more sweat (S) when body temperature (H) is not maintained at normal levels due to a certain phenomenon (T). Since this structure helps to maintain H in equilibrium, it will tend to be selected or reinforced.
Stinchcombe’s diagram may be intuitively mapped onto familiar neighbourhood dynamics. For example, we may treat as Homeostatic (H) variables neighbourhood character, style, or scene (such as distinctive shops, restaurants, venues, or groups), Tension (T) variables as pressures to change that character (from, for example, new groups with divergent tastes), and Structure (S) variables as activities that maintain that character (such as Business Improvement Association sponsored festivals, political advocacy, or increased participation in venues and activities distinctive to that scene).
Based on this simple representation, we formulate an initial set of propositions regarding the presence and strength of 1) a functional relationship and 2) a homeostatic response, which can be seen in the paper in more detail.
The key value of such models from the point of considering urban evolution is that treat both persistence and change as a dynamic process. Urban forms of life are retained when there exist structures that preserve them when new challenges. If such structures respond effectively to tensions, there is a tendency for them to be selected and reinforced over time, generating both a pattern of structural retention and possible evolutionary histories of such structures. This idea is scarred further in Part III of “Towards a Model of Urban Evolution,” in our discussion of “retention hypotheses.”
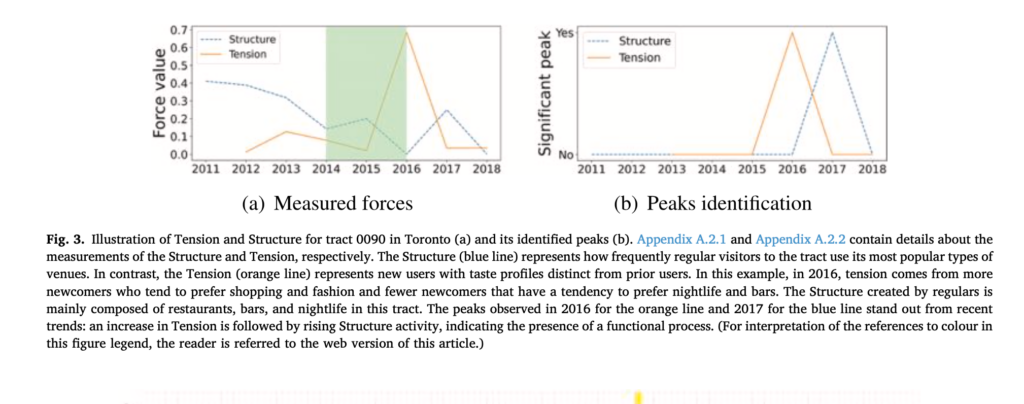
Using data drawn from Yelp.com, we find considerable evidence that the sort of functional process envisaged in the model is a common feature of urban evolution. And in the process we develop novel methods for using data from Yelp and similar sources for such analyses.
We see great potential for using these models and methods for characterizing neighbourhoods in new ways. In contrast to the typical approach, which does so primarily by their demographics or built form, our proposed functionalist approach would identify neighbourhoods with more or less latent potential to resist tensions. In this way, neighbourhoods that look otherwise similar could be shown to have very different probabilities of maintaining their identity over time, thereby allowing planners and policymakers to take these latent functional capacities into account.
While incorporating novel data sources and methods would, to some extent, be challenging, doing so would be in line with parallel proposals. Indeed, local jurisdictions routinely use big data in multiple ways: traffic demand management (using GPS and sensor data), land use (using remotely sensed data), public health (COVID sewage testing), commercial health (using payments data), and more. Our methods could be used in a similar way to monitor tendencies toward neighbourhood change.
From the point of view of social science research more generally, perhaps the biggest result of our study is the possibility of reviving interest in functional explanation. While functional explanation has been characterized as “what any science does,” it has largely fallen out of favour in social science. We review common criticisms, and show that they do not apply to a properly specific functional model of the sort we propose.
At the same time, we find considerable evidence that functionalist motifs are commonplace in neighborhood change research. Researchers typically appeal to functionalist motifs when they discuss for example the capacity of local groups to push back against tensions or challenges as a key mechanism producing continuity or change. However, we found no examples in the neighbourhood change literature where an author who utilized a functionalist motif articulated the motif in an explanatory model that would render it testable. Instead, much neighbourhood change research remains largely descriptive, mapping types and directions of change across a range of variables.
We hope one result of our study is to illustrate a path for remedying this situation, which in turn would help to more formally incorporate evolutionary thinking into urban research.


Leave a Reply
You must be logged in to post a comment.