line
Generative models of urban form
In Venues and segregation: A revised Schelling model we demonstrate that venues can play a crucial role in shaping urban evolution, in particular through influencing broader patterns of integration and segregation. Due to space considerations, we could not include a key study in the paper.
This study investigates whether and how venues can diversify a segregated city after it a particular segregation pattern has become deeply entrenched. To answer this question, we first simulate a highly segregated city as an outcome of a standard Schelling process. Then we use a genetic algorithm to evolve the set of rules that would most decrease the degree of segregation. These rules include the location of venues, their exclusivity, and their degree of obligatoriness. In effect, the study evolves rules that would most dramatically alter the evolutionary direction of a city.
The study is below. See the original paper for more details regarding the parameters and graphical conventions, and simulation rules.
Venues can unsettle sedimented patterns of segregation under certain conditions.
In this study, we demonstrate that the strategic placement of a new venue can unsettle sedimented patterns of segregation. This is important because one of the characteristics of the segregation patterns generated in Schelling simulations is that they are highly uni-directional processes. Once a set of individuals has become segregated, even a significant increase in their tolerance will not undo the neighbourhood divisions that have taken shape – barring any modifications to the internal psychology of individuals within the simulation. In this study, we show that venues can be used as an intervention within a settled Schelling model in order to disrupt the segregated outcome, without requiring any change to agents’ psychology. To do so, we add venues to a venue-less simulation that has already run its course and achieved a high level of segregated stability. In order to effectively determine what input parameters and venue positions will provide the most disruption, the two-dimensional parameter spaces used to explore earlier studies is not sufficient. Here we consider a range of venue positions, exclusivity, obligatoriness, tolerance, travel distance, and neighbourhood distance values simultaneously. In lieu of our prior interval based approach, we employ a Genetic Algorithm to test and recombine values for these parameters, evaluating different combinations in terms of how much they disrupt the initial condition (measured as a drop in concordance from the initial, segregated condition). An additional mechanism emerges, whereby one group’s venue establishes a “beachhead” into an area predominated by the other.
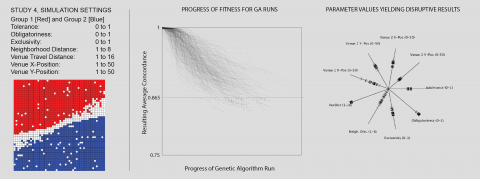
Figure 1 displays results. After running the algorithm with a variety of population sizes, mutation rates, and crossover rates, the progress of each evolutionary process is mapped as a sequence of fitness values to the chart in center of Fig 1. Here, movement towards the right along each thread indicates the progress of the algorithm during one of its runs, while dropping values on the Y-axis indicate a reduction in the resulting concordance, i.e. a more successful solution. We select the most successful interventions in order to compare their values for each input parameter in the chart to the right in Fig 1. Here, each notch along one of the spokes indicates a parameter value for one of the interventions, and hence, each intervention can be composed from a set of notches on each of the spokes.
FIG 1 HERE
Beginning from “Intolerance” and working clockwise through the spokes on Fig. 1, we consider the significance of the values arrived at for each, highlighting values that contribute to disruptive solutions. Overall, these solutions cluster around medium-low intolerance levels, high obligatoriness, middling exclusiveness, high catchment areas, a wide range of neighbourhood distances, and “beachhead” venue positions.
Intolerance: The intolerance values are clustered tightly around the value of 0.4 in successfully disruptive solutions. This value, just above the traditional Shelling tipping point, can be understood as a trade-off: it is high enough to motivate some movement by individuals, but low enough to support these same agents moving to an integrated rather than segregated destination.
Obligatoriness: The obligatoriness values tend towards 1 in disruptive solutions. Since obligatoriness controls the fraction of individuals that will feel compelled to visit venues, and since venues are the mechanism for disrupting the settled state, it follows that maximizing venue attendance will maximize the potential disruption. By contrast, introducing venues that inspire no obligation to attend them will do little to alter a segregated condition.
Exclusivity: Since exclusivity controls the number of other-group individuals who will consider visiting a venue, it regulates the new encounters between the segregated groups. It follows that an exclusivity of less than 1 is necessary in order to yield any new outcomes. On the other hand, if the exclusivity is too low, any agents within the travel distance would visit and it would hence replicate the distribution of the surrounding area. Between these extremes, and in fact closer to an exclusivity range from 0.4 to 0.6, we have circumstances in which some individuals of the opposite group will be drawn into a venue, leading to a disruption when they find that after visiting they are no longer comfortable with their location. Thus maximizing disruption involves introducing venues that are neither too exclusive nor too open but rather those that exist in a “sweet spot” between the two extremes.
Neighbourhood Distance: The neighbourhood distance is the most dispersed of the non-location parameters, with all of its distribution occurring below a value of 4. We interpret this to imply that neighbourhood distance does not play a significant role in the outcome, so long as it is sufficiently low.
Venue Travel Distance: Unlike neighbourhood distance, the venue travel distance is very tightly clustered, and tends towards the highest value possible. Since venue travel distance directly determines the number of individuals who can be affected by the venues, higher values naturally yield more disruptive results. Thus introducing venues with large catchment areas is likely crucial to interventions designed to unsettle existing patterns of segregation.
Venue Positions: Each of the two venues’ positions are encoded as an X and Y value between 1 and 50. This allows them to be located anywhere in the simulation world, even if this means displacing an individual from their initial condition. While their positions in successful solutions are mostly constrained to a narrow range, the X position of the first venue is something of an exception – with a whole range of positions that yield disruptions. In Fig 2, we summarize our findings for the venues’ positions by stepping through each cell, finding any simulations in which one of the venues occupies this cell, and colouring the cell according to the most disruptive outcome from among these simulations. In other words, we colour each square according to a best-case scenario of having a venue located there. What results is a map of the most effective positions for locating venues.
FIGURE 2 HERE
Venues at “beachheads” are most likely to disrupt stable segregation patterns.Though the central map of Fig 2 clearly illustrates that there is a broad band of more successful venue locations along the boundary area between the two segregated groups, closer inspection reveals that ideal positions tend to be slightly embedded within one of the groups, rather than in the unoccupied space between. The tight clustering of values for the other parameters suggest that the successful disruptive runs are all variations on a single, emergent, strategy. This strategy involves locating a relatively open venue of a group (G1) near to the edge but slightly embedded within the segregated neighbourhood of the opposite group (G2). Because of the high maximum travel distance, individuals from the G1 are able to visit from farther away, while some closer agents from G2 are welcomed by the low exclusivity. Upon visiting, these G2 agents become less comfortable with their location, since attendance has exposed them to a greater number of agents from G1. Simultaneously, the opposite dynamic is unfolding somewhere else in the simulation world. Because of this symmetry, individuals from both groups who feel compelled to move will find new locations opening up within travel distance to an appropriate venue, leading to an exchange between two areas of the simulation world. Since the venue exclusivity is not too low, this exchange is not a complete flip – only the fraction of individuals who visit the opposite venue will relocate. These venues act like a “beachhead”, pushing away individuals from the other group and opening up spaces for their own agents to occupy. We can watch this same dynamic unfolding in the Video.
Summary
In this study, we consider the possibility of applying our venue model as an intervention in highly segregated conditions. The success of the genetic algorithm in finding highly disruptive venue configurations speaks to the potential role for planning and design as a means of re-integrating a divided urban condition. It must be stressed that the successful strategy described in this study is specifically tuned to the particular starting conditions that were used. Nonetheless, this study points at specific spatial relationships between segregated groups and disruptive venues as well as the crucial balancing of parameters such as intolerance and exclusivity. Further research would be necessary to generalize these results for other kinds of initial distributions of the simulated population.




